

This means that the function has the same value for x and -x. This makes sense because we reflect functions over the x-axis by multiplying them by a negative. If a is negative, the parabola points downwards. If a is positive, the parabola turns upwards. We know whether the parabola of our quadratic function will turn upwards or downwards based on the value of a. Note that concave parabolas may also be known as concave up and convex parabolas may also be known as concave down. On the other hand, the y-values of the latter will extend to negative infinity as x goes towards positive or negative infinity. Solutions of the former will extend to positive infinity as x goes towards positive or negative infinity. We call parabolas that curve upwards “concave” and parabolas that curve downward convex.

ShapeĮvery parabola will turn upwards like a smiley face or turn downwards like a frown. In particular, we are interested in the vertex, the y-intercept, the x-intercept(s), and the general shape of the graph. When a is not equal to 0, however, we need to use the values of a, b, and c to tell us about the graph. If the value of a is 0, then we simply have a linear function and can graph it like any other linear function. Recall that quadratic functions have the form ax 2+bx+c, where a, b, and c are real numbers. Make sure to review these concepts before moving forward. Graphing quadratics requires a solid understanding of coordinate geometry and graphing. Mathematically, such functions are called concave and convex or “concave up” and “concave down.”
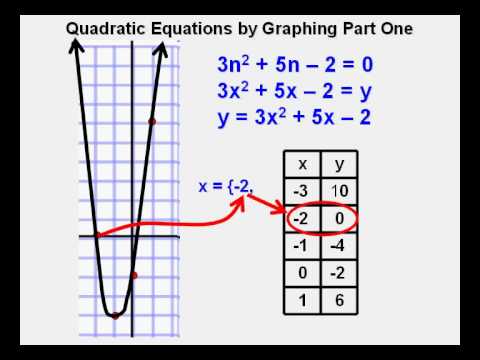
The parabolic shape is often likened to a smiley face or a frowning face. These functions will generally form a parabola. Graphing quadratic functions models an x 2 function in two-dimensional space.


 0 kommentar(er)
0 kommentar(er)
